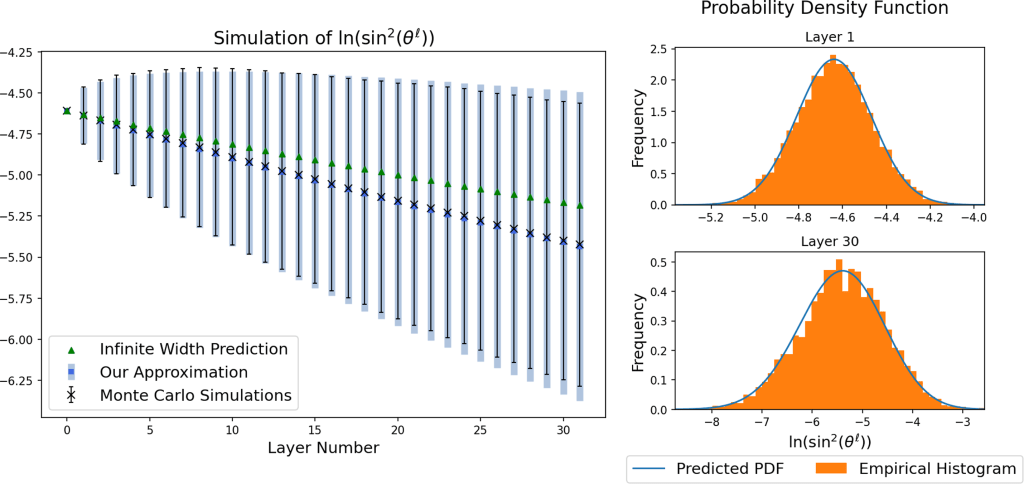
This paper (accepted to the Journal of Machine Learning Research) is the main project I have worked on throughout my Master’s degree, under the supervision of Dr. Mihai Nica (Professor of Mathematics, University of Guelph). We study the phenomenon of “depth degeneracy” in ReLU neural networks upon initialization. Adding layers to make networks “deeper” can greatly improve the expressibility of the network, but as networks become deeper, the network can have a harder time differentiating between inputs. In other words, inputs become more correlated as they travel layer to layer. This is an issue, because if you make your network too deep, it effectively can’t tell the difference between inputs when initialized, and therefore will have a hard time training properly.
We study this phenomenon in the paper below, and come up with a simple update rule to predict the correlation between 2 inputs as they travel through the network. We also introduce formulas to predict the mean and variance of the angle, which allow us to accurately predict the joint distribution of 2 inputs into a ReLU network given its architecture.
This paper can be found here, and code used to produce Figure 1 can be found on my GitHub.