This is a project I completed for a fourth year undergraduate research course, under the supervision of Dr. Rajesh Pereira (Professor of Mathematics, University of Guelph). Our work studies the quotient l-infinity norm and its relation to Hilbert’s projective metric. We are able to characterize Hilbert’s metric in a simple way using this norm, which allows us to easier study topological properties of sets under Hilbert’s metric, leading to a simplification in the proof of the Perron-Frobenius theorem.
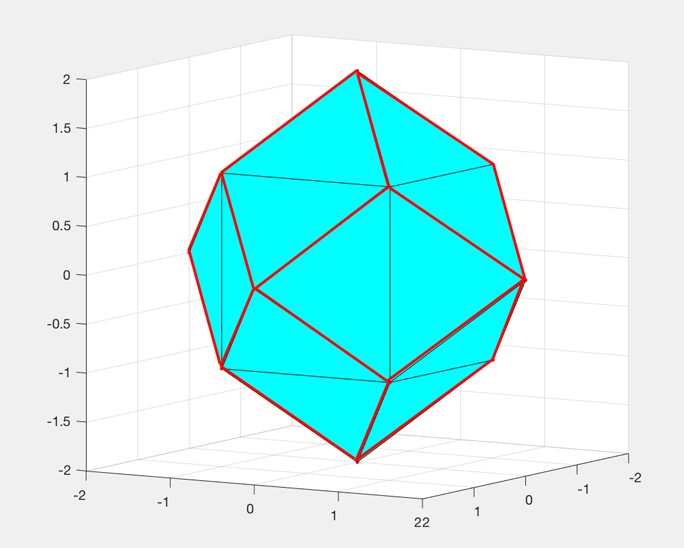
We also study the “shape” of the unit ball for the quotient l-infinity norm in higher dimensions. We found that the quotient l-infinity unit ball in 4 dimensions is the rhombic dodecahedron (pictured above), which quickly became my favourite shape! The full report is included below.